AI Research Review 25.02.13
Scaling up Test-Time Compute with Latent Reasoning, Compute-Optimal Test-Time Scaling, OREAL Outcome-based RL for Reasoning, demystifying CoT, LIMO: Less is more for reasoning.

Introduction
This week’s AI Research Review covers several recent papers that are exploring AI reasoning, in particular with innovations in test-time scaling – using latent reasoning and optimal policy-guided scaling – as well as improving reasoning with innovations in RL:
Scaling up Test-Time Compute with Latent Reasoning: A Recurrent Depth Approach
Can 1B LLM Surpass 405B LLM? Rethinking Compute-Optimal Test-Time Scaling
OREAL: Exploring the Limit of Outcome Reward for Learning Mathematical Reasoning
Demystifying Long Chain-of-Thought Reasoning in LLMs
LIMO: Less is More for Reasoning
One simple conclusion of these various results is that AI reasoning models have room for improvement in efficiency, in the RL training and in the use test-time compute scale.
Scaling Test-Time Compute with Latent Reasoning
By constructing an architecture that is compute-heavy and small in parameter count, we hope to set a strong prior towards models that solve problems by “thinking,” i.e., by learning meta-strategies, logic and abstraction, instead of memorizing. - From Scaling up Test-Time Compute with Latent Reasoning: A Recurrent Depth Approach
AI models can reason more effectively if they are not restricted to having to ‘think’ through tokens. The paper Scaling up Test-Time Compute with Latent Reasoning: A Recurrent Depth Approach uses a modified LLM transformer architecture that scales reasoning compute in its latent space. Unlike existing models that increase computation by producing more tokens, this model employs a recurrent block, enabling it to unroll to arbitrary depths during inference.

The authors developed a 3.5 B proof-of-concept model called Huggin, trained on 800 billion tokens, and demonstrated improved performance on reasoning benchmarks, equivalent to models an order of magnitude larger. As the latent depth-recurrent block iterations rise during inference, the performance rises, as shown on various benchmarks.

This approach operates with small context windows and captures reasoning types that are not easily verbalized in tokens. More importantly, it presents an AI reasoning technique that is general, powerful, and more efficient. The authors have shared the model on HuggingFace and code and data on GitHub.
Can 1B LLM Surpass 405B LLM? Rethinking Compute-Optimal Test-Time Scaling
The paper “Can 1B LLM Surpass 405B LLM? Rethinking Compute-Optimal Test-Time Scaling” explores the effectiveness of Test-Time Scaling (TTS) in enhancing LLM performance on complex reasoning. The study investigates how policy models, Process Reward Models (PRMs), and problem difficulty interact to influence TTS strategies.
Through experiments on MATH-500 and AIME24 datasets, the authors find that compute-optimal TTS is highly dependent on the choice of policy model, PRM, and problem difficulty. As with the prior paper, they found methods that could elicit extremely high AI reasoning performance out of small AI models:
For example, a 1B LLM can exceed a 405B LLM on MATH-500. Moreover, on both MATH-500 and AIME24, a 0.5B LLM outperforms GPT-4o, a 3B LLM surpasses a 405B LLM, and a 7B LLM beats o1 and DeepSeek-R1.
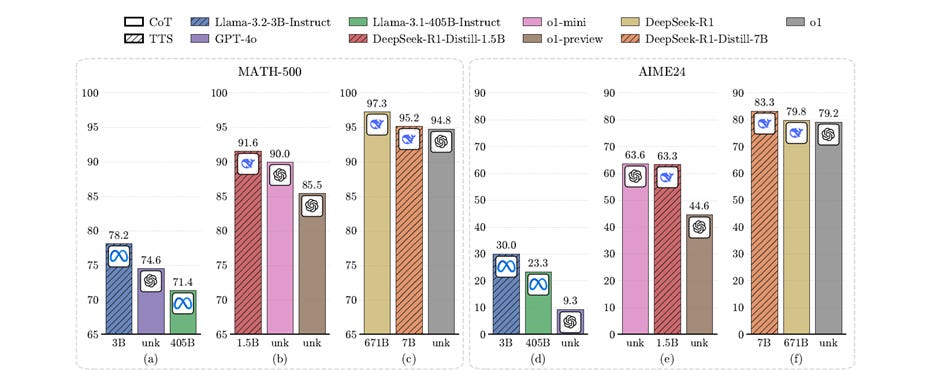
A key contribution that led to this result is the introduction of a "reward-aware" compute-optimal TTS strategy, which integrates reward information into the scaling process, adapting to the policy model, prompt, and reward function.
The study demonstrates that smaller LLMs can outperform larger models with compute-optimal TTS, adapting TTS strategies to the specific characteristics of each task strategically allocating additional computation at inference time. It also shows there is room for improvement in the efficiency of test-time scaling for AI reasoning.
OREAL: Exploring the Limit of Outcome Reward for Learning Mathematical Reasoning
The paper Exploring the Limit of Outcome Reward for Learning Mathematical Reasoning introduces OREAL, a novel outcome-reward-based reinforcement learning (RL) framework designed to enhance the mathematical reasoning capabilities of LLMs. OREAL addresses the challenge of sparse rewards in mathematical problem-solving, where only the correctness of the final answer provides feedback.
They first derived a theoretical result: Behavior cloning on positive trajectories from Best-of-n (BoN) sampling is both necessary and sufficient for optimal policy learning under binary feedback.
They use this and additional observations to develop OREAL, a theoretically grounded and scalable RL algorithm to train AI models for mathematical reasoning tasks. They trained OREAL 7B and 32B models (from Using Qwen2.5 7B and 32B base models) using their OREAL RL algorithm. Experiments on the MATH-500 dataset demonstrate that OREAL significantly improves the mathematical reasoning abilities of LLMs, beating o1-mini on several benchmarks.

OREAL establishes a theoretical basis for outcome-reward policy modeling for RL for AI reasoning. It also confirms the result of DeepSeek R1, showing that a properly designed outcome-reward-based RL is sufficient to train a model for AI reasoning.
Demystifying Long Chain-of-Thought Reasoning in LLMs
Long chain-of-thought (CoT) reasoning in LLMs enable strategies like backtracking and error correction, crucial for complex tasks. The paper Demystifying Long Chain-of-Thought Reasoning in LLMs investigates the mechanics behind long Chain-of-thought, exploring supervised fine-tuning (SFT) and reinforcement learning (RL) to understand how LLMs generate extended reasoning trajectories.
The authors conducted extensive supervised fine-tuning (SFT) and RL experiments on Llama-3.1-8B and Qwen2.5-7B-Math models to establish these four main findings:
(1) While SFT is not strictly necessary, it simplifies training and improves efficiency.
(2) Reasoning capabilities tend to emerge with increased training compute, but their development is not guaranteed, making reward shaping crucial for stabilizing CoT length growth.
(3) Scaling verifiable reward signals is critical for RL. We find that leveraging noisy, web-extracted solutions with filtering mechanisms shows strong potential, particularly for out-of-distribution (OOD) tasks such as STEM reasoning.
(4) Core abilities like error correction are inherently present in base models, but incentivizing these skills effectively for complex tasks via RL demands significant compute, and measuring their emergence requires a nuanced approach.
The paper offers practical insights for optimizing training strategies to improve long CoT reasoning in LLMs. Findings, like the need for proper reward shaping, both confirm and overlap with other papers mentioned.
LIMO: Less is More for Reasoning
We present a fundamental discovery that challenges our understanding of how complex reasoning emerges in large language models. While conventional wisdom suggests that sophisticated reasoning tasks demand extensive training data (>100,000 examples), we demonstrate that complex mathematical reasoning abilities can be effectively elicited with surprisingly few examples. - LIMO: Less is More for Reasoning
The paper LIMO: Less is More for Reasoning introduces the Less-Is-More Reasoning Hypothesis (LIMO), challenging the conventional reliance on massive datasets for training complex reasoning in large language models (LLMs).
The LIMO hypothesis posits that with sufficient domain knowledge encoded during pre-training, sophisticated reasoning can emerge from minimal, carefully designed demonstrations of cognitive processes. This depends on (1) the completeness of the model’s encoded knowledge foundation during pre-training and (2) the effectiveness of post-training examples as "cognitive templates" for problem-solving.
The authors were able to achieve remarkable results from just a small number of curated RL training samples, validating the LIMO hypothesis:
With merely 817 curated training samples, LIMO achieves 57.1% accuracy on AIME and 94.8% on MATH, improving from previous SFT-based models' 6.5% and 59.2% respectively, while only using 1% of the training data required by previous approaches. LIMO demonstrates exceptional out-of-distribution generalization, achieving 40.5% absolute improvement across 10 diverse benchmarks, outperforming models trained on 100x more data, challenging the notion that SFT leads to memorization rather than generalization.
The paper contrasts LIMO with reinforcement learning (RL) scaling approaches, arguing that LIMO directly constructs reasoning trajectories, while RL scaling searches for them. This leads to vastly more efficient training in LIMO.




