Our AI research highlights for this week focus on several topics - vision-language and multi-modal models, scaling laws, 4D generations from video, and advances in theory-of-mind and arithmetic with LLMs:
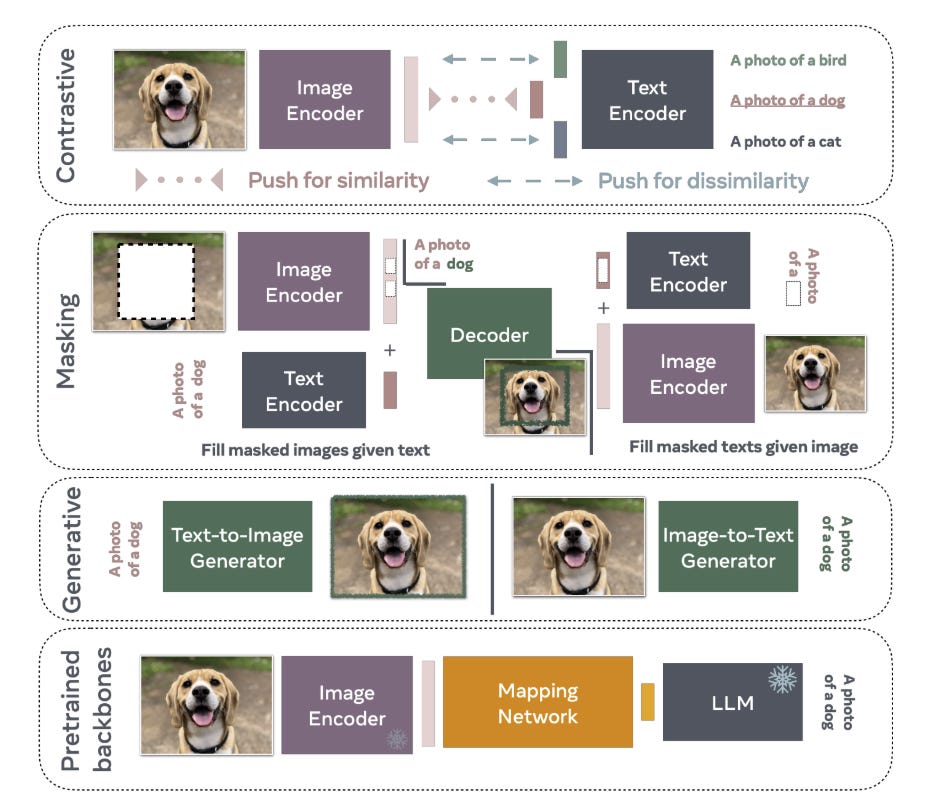
An Introduction to Vision-Language Modeling
ConvLLaVA: Hierarchical Backbones as Visual Encoder for Large Multimodal Models
Matryoshka Multimodal Models
RLAIF-V: Aligning MLLMs through Open-Source AI Feedback for Super GPT-4V Trustworthiness
GFlow: Recovering 4D World from Monocular Video
Observational and Data-dependent Scaling Laws
Gzip Predicts Data-dependent Scaling Laws
Observational Scaling Laws and the Predictability of LLM Performance
Transformers Can Do Arithmetic with the Right Embeddings
LLMs achieve adult human performance on higher-order theory of mind tasks
An Introduction to Vision-Language Modeling
An Introduction to Vision-Language Modelingis a introductory paper giving an overview of Vision-Language Models (VLMs); what VLMs are, how they work, how to train them, and how to evaluate VLMs.
Figure 2. Types of VLMs - Contrastive, masking, generative, and pretrained backbones.
As shared in Figure 2, there are several types of VLMs, and a variety of applications for these models. They primarily focuses on mapping images to language, but also discuss extending VLMs to videos. This is not a full survey of the VLM field, but it is a good introduction for those needing to better understand the mechanics behind mapping vision to language in AI models.
ConvLLaVA: Hierarchical Backbones as Visual Encoder for Large Multimodal Models
To handle high-resolution images, LMMs using Vision Transformer (ViT) for vision encoding require excessive visual tokens and quadratic visual complexity. Methods to address the quadratic complexity of ViTs still generate excessive visual tokens.
Figure 3. Architecture for (a) LLaVA and (b) ConvLLaVA and ( c) training procedure.
To address these issues, ConvLLaVA employs ConvNeXt, a convolutional vision encoder, in a 5-stage hierarchical backbone, as the visual encoder of LMM to replace Vision Transformer (ViT). The ConvNeXt hierarchy compresses the visual tokens and reduces redundancy. It uses a two-layer MLP and Vicuna-7B as the projector and language model, following LLaVA-1.5:
These optimizations enable ConvLLaVA to support inputs of 1536x1536 resolution generating only 576 visual tokens, capable of handling images of arbitrary aspect ratios.
ConvLLaVA achieves competitive performance with state-of-the-art models on mainstream benchmarks:
Our 7B parameter model exhibits superior performance compared to the LLaVA-1.5 13B model.
Matryoshka Multimodal Models
The paper Matryoshka Multimodal Modelsconsiders also the challenge to LMMs mentioned above: “an excessive number of tokens for dense visual scenarios such as high-resolution images and videos.”
Their solution is based on the concept of Matryoshka Dolls, using controllable hierarchy to reduce redundant information:
M3: Matryoshka Multimodal Models … learns to represent visual content as nested sets of visual tokens that capture information across multiple coarse-to-fine granularities.
Figure 4. The M3 process with granularity controller adapting the level of output detail.
Their M3 architecture starts with a LMM that combines a CLIP-based image encoder and language model (LLM). It allows control over the visual granularity per test instance during inference, e.g. , adjusting the number of tokens used to represent an image based on the anticipated complexity or simplicity of the content.
As such, M3 “provides a framework for analyzing the granularity needed for existing datasets,” and it can help “explore the best trade-off between performance and visual token length at sample level.”
Figure 5. Potential variable detail output from M3.
RLAIF-V: Aligning MLLMs through Open-Source AI Feedback
RLHF, reinforcement learning with human feedback, is based on text prompts. RLAIF uses AI model labelling to automate the RLHF process. RLAIF-V extends RLAIF to vision data and aligns MLLMs in an open-source way:
RLAIF-V maximally exploits the open-source feedback from two perspectives, including high-quality feedback data and online feedback learning algorithm.
Figure 6. the RLAIF-V process.
They showed RLAIF-V enhances the trustworthiness of models through experiments applying RLAIF-V on LLaVA-1.5:
Using a 34B model as labeler, RLAIF-V 7B model reduces object hallucination by 82.9% and overall hallucination by 42.1%, outperforming the labeler model. Remarkably, RLAIF-V also reveals the self-alignment potential of open-source MLLMs, where a 12B model can learn from the feedback of itself to achieve less than 29.5% overall hallucination rate, surpassing GPT-4V (45.9%) by a large margin.
We introduce GFlow, a new framework that utilizes only 2D priors (depth and optical flow) to lift a video (3D) to a 4D explicit representation, entailing a flow of Gaussian splatting through space and time.
The Gaussian splatting is a 3D representation, so a time-line of 3D Gaussian splats gives you a 4D representation. How it works:
GFlow first clusters the scene into still and moving parts, then applies a sequential optimization process that optimizes camera poses and the dynamics of 3D Gaussian points based on 2D priors and scene clustering, ensuring fidelity among neighboring points and smooth movement across frames.
Figure 7. GFlow steps from (a) monocular video input to (b) reconstructed gaussians to (c ) downstream video applications
Having a full 4D representation on hand has a number of useful applications, from automated vehicles to video editing and reconstruction. The authors mention that GFlow artifacts allow for rendering novel views of a video scene through changing camera pose.
They have a project website for GFlow here, but have not yet released code.
Observational and Data-dependent Scaling Laws
Two papers are looking at scaling laws, to understand and predict LLM capability based on input parameters, training data, and compute.
Building a single scaling law from multiple model families is challenging due to large variations in their training compute efficiencies and capabilities. However, we show that these variations are consistent with a simple, generalized scaling law where language model performance is a function of a low-dimensional capability space, and model families only vary in their efficiency in converting training compute to capabilities.
Figure 8. Framework for the observational scaling laws.
They show that “several emergent phenomena follow a smooth, sigmoidal behavior and are predictable from small models.” Examples are shown in Figure 9.
Figure 9. Emergent behavior can be modeled and predicted with (a) FLOP based scale and (b) observational scaling laws.
Another form of prediction comes from considering LLMs as compressors of knowledge. The paper gzip Predicts Data-dependent Scaling Laws proposes a data-dependent scaling law for LLMs that accounts for the training data's gzip-compressibility:
We generate training datasets of varying complexities, finding that
1) scaling laws are sensitive to differences in data complexity, and
2) gzip, a compression algorithm, is an effective predictor of how data complexity impacts scaling properties.
Data quality matters in training datasets, as results from Phi models show us. gzip compressibility is a useful metric to help understand which mix and types of data is more effective in LLM training datasets.
Transformers Can Do Arithmetic with the Right Embeddings
We mend this problem by adding an embedding to each digit that encodes its position relative to the start of the number.
From there, they asked “Can they solve arithmetic problems that are larger and more complex than those in their training data?”
We find that training on only 20 digit numbers with a single GPU for one day, we can reach state-of-the-art performance, achieving up to 99% accuracy on 100 digit addition problems.
It’s interesting that simply giving the LLM knowledge of specific ordering of digits in numbers fixes its confusion enough to do so much better. Improving their arithmetic capabilities also unlocks some multi-step reasoning tasks including sorting and multiplication.
In a similar manner, LLMs do poorly on some word-play challenges like palindromes and crossword-puzzles. If they were trained on character-level tokens, letters, and spellings, etc. they might understand and solve problems requiring letter-level understanding.
LLMs achieve adult human performance on theory of mind tasks
We find that GPT-4 and Flan-PaLM reach adult-level and near adult-level performance on ToM tasks overall, and that GPT-4 exceeds adult performance on 6th order inferences.
LLMs having a high-order theory-of-mind is an important capability. It opens the door to important reasoning capabilities and is helpful in developing better AI assistants.
Thanks for reading AI Changes Everything! Subscribe for free to receive new posts and support my work.
