AI Research Roundup 24.11.16: Reasoning
Limits and advances in AI Reasoning: GSM-Symbolic, Test-Time Training (TTT), ScaleQuest, Entropix, SMART, the Talker-Reasoner architecture.

Introduction
This week, our Research Roundup covers Reasoning in AI models and agents, both their limits and opportunities to help improve AI model reasoning:
GSM-Symbolic: The Limits of Mathematical Reasoning in LLMs
TTT: The Surprising Effectiveness of Test-Time Training for Abstract Reasoning
ScaleQuest: Unleashing Reasoning Capability of LLMs via Scalable Question Synthesis
Entropix: Overcoming Limitations of Mathematical Reasoning in LLMs
SMART: Self-learning Meta-strategy Agent for Reasoning Tasks
Agents Thinking Fast and Slow: A Talker-Reasoner Architecture
GSM-Symbolic: The Limitations of Mathematical Reasoning in LLMs
How well can AI models reason? Not very well, according to a recent paper that exposed some of the limitations and ‘fragility’ of reasoning in LLMs.
A huge challenge in evaluating AI reasoning is trying to distinguish formal reasoning processes from merely pattern-matching. The paper GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models investigates the limitations of LLMs in mathematical reasoning, particularly focusing on the widely used GSM8K benchmark. The authors argue that current evaluations using GSM8K offer limited insights due to its fixed question set and potential data contamination. LLMs can get answers right not by abstract reasoning but by pattern-matching over reasoning steps, passing benchmarks while falling short of true logical reasoning.
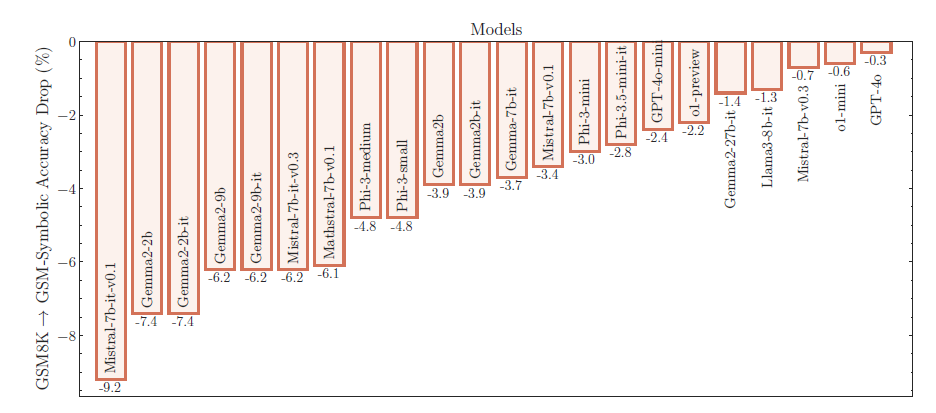
To address this, they introduce GSM-Symbolic, a new benchmark derived from symbolic templates that allows for generating diverse problem instances. GSM-Symbolic was used to evaluate leading LLMs in controlled experiments by varying numerical values and superficial elements like names within questions, while maintaining the underlying mathematical structure.
The results showed significant drop-off in performance on variations of original GSM-8K questions:
Our findings reveal that LLMs exhibit noticeable variance when responding to different instantiations of the same question. Specifically, the performance of all models declines when only the numerical values in the question are altered in the GSM-Symbolic benchmark … their performance significantly deteriorates as the number of clauses in a question increases.
The drop due to changes in numerical values suggests data contamination, while the drop due to more clauses - up to 65% drop from adding irrelevant clauses - suggests problems with reasoning and ability to distinguish between relevant and irrelevant data.
We hypothesize that this decline is because current LLMs cannot perform genuine logical reasoning; they replicate reasoning steps from their training data.
The findings highlight the fragility of current LLM reasoning abilities. Notably, the GPT-4o and o1 models suffered smaller drop-offs than the smaller models. It could be that distilled LLMs can distill patterns of output from larger AI models but not logical reasoning capabilities. The smaller LLMs seem more fragile.
Finally, a new dataset, GSM-NoOp, was introduced, which adds information that seems to be relevant but is actually irrelevant to questions. This resulted in substantial performance drops (up to 65%), revealing a critical weakness in the models’ ability to discern relevant information. Even with in-context examples demonstrating the irrelevance of the added information, LLMs failed to improve, indicating a fundamental limitation in their reasoning process, potentially stemming from a reliance on pattern matching rather than true logical deduction.
“The high variance in LLM performance on different versions of the same question, their substantial drop in performance with a minor increase in difficulty, and their sensitivity to inconsequential information indicate that their reasoning is fragile. It may resemble sophisticated pattern matching more than true logical reasoning.” – GSM-Symbolic paper
When it came out in early October, this paper caused quite a stir among AI commentators. Gary Marcus had the blunt assessment: LLMs don’t do formal reasoning - and that is a HUGE problem. Overall, LLMs are at their core sequential token generators, which is great for word generation but is a poor fit for complex mathematical reasoning.
These LLM limitations are significant but not unsurmountable. Recent papers shared below show various approaches to improve AI model reasoning and mitigate LLM limitations in reasoning.
TTT: The Surprising Effectiveness of Test-Time Training for Abstract Reasoning
The paper The Surprising Effectiveness of Test-Time Training for Abstract Reasoning from researchers at MIT tackles the challenge of improving reasoning capabilities of language models. They develop methods for test-time training (TTT) and investigate its effectiveness for improving reasoning, using the Abstraction and Reasoning Corpus (ARC) as a benchmark.
Test-time training or TTT is a technique where the model parameters are temporarily updated during inference using the input data. Like the test-time compute approach used in the o1 model, TTT applies effort during inference to solve hard problems, with specific attention to fine-tuning the AI model for the task. The authors identify three crucial elements in TTT:
(1) initial fine-tuning on similar tasks,
(2) an augmented, leave-one-out task generation strategy, and
(3) per-instance adapter training.
TTT performs remarkably well on the ARC benchmark, achieving SOTA results that improve scores 6-fold over the same base models:
applying TTT to an 8B-parameter language model, we achieve 53% accuracy on the ARC's public validation set, improving the state-of-the-art by nearly 25% for public and purely neural approaches. By ensembling our method with recent program generation approaches, we get SOTA public validation accuracy of 61.9%, matching the average human score.
The TTT approach uses a variety of ways to ask similar symmetric problems and used additional test-time applied to continued training on few-shot examples. These techniques proved to be “unreasonably effective” and show that creative ways of using inference-time compute beyond direct explicit symbolic search can unlock more reasoning capabilities.
ScaleQuest: Unleashing Reasoning Capability of LLMs via Question Synthesis
Improving LLM reasoning capabilities requires sufficient high-quality training data. For example, creating instructions from seed questions, or synthesizing data from strong models (e.g., GPT-4) to use in fine-tuning can improve AI model reasoning.
The paper Unleashing Reasoning Capability of LLMs via Scalable Question Synthesis from Scratch presents ScaleQuest, a scalable, cost-effective method for synthesizing data that yields a large dataset for improving mathematical reasoning. ScaleQuest generates questions from scratch using smaller, open-source LLMs (e.g., 7B), significantly reducing the reliance on expensive APIs like GPT-4. The authors claim:
With the efficient ScaleQuest, we automatically constructed a mathematical reasoning dataset consisting of 1 million problem-solution pairs, which are more effective than existing open-sourced datasets.
The ScaleQuest method comprises a two-stage question-tuning process. First, Question Fine-Tuning (QFT) activates the model's question generation capability by training it on a small mixed dataset of problems (without solutions) from GSM8K and MATH. Second, Question Preference Optimization (QPO) refines the generated questions, using an external LLM (GPT-4o-mini) to optimize a set of generated questions for either solvability or difficulty. A filtering pipeline ensures quality, removing non-English questions, illogical or unanswerable questions, and sampling for appropriately challenging questions.
Finally, with the questions developed, responses are generated using Qwen2-Math-7B-Instruct with chain-of-thought prompting. Multiple solutions are generated per question, with the highest-scoring solution according to a reward model (InternLM2-7B-Reward) selected for the final dataset.
Experiments demonstrate a ScaleQuest generated dataset of 1 million question-answer pairs significantly boosted performance (29.2% to 46.4%) across various open-source LLMs (Mistral-7B, Llama3-8B, DeepSeekMath-7B, Qwen2-Math-7B) on four mathematical reasoning benchmarks.
Notably, simply fine-tuning the Qwen2-Math-7B-Base model with our dataset can even surpass Qwen2-Math-7B-Instruct, a strong and well-aligned model on closed-source data, and proprietary models such as GPT-4-Turbo and Claude-3.5 Sonnet.
Entropix: Overcoming Limitations of Mathematical Reasoning in LLMs
Entropix is an open-source project on GitHub that aims to mimic advanced reasoning in small LLMs through a sampling technique. They don’t have a paper published, but we can learn a bit about what Entropix is attempting to do in their GitHub Readme and a review by Tim Kellogg.
There are many ways sampling can be used to improve LLM performance that involve generating then selecting from multiple outputs. For example, a majority voting sampling technique generates multiple answers and takes a majority vote or selection on them.
Entropix introduces a novel sampling technique aimed at boosting the reasoning capabilities by looking at the amount of uncertainty in the answer on a token-by-token basis. They introduce two concepts: entropy, as a state of uncertainty in an answer, and varentropy, the variance in that uncertainty. They explain varentropy as:
High varentropy means I'm considering vastly different futures, different tones and directions. Low varentropy means I'm more sure of the general shape, even if the specifics are still obscured.
Entropix doesn't retrain or fine-tune models but adds code to token-generation step to enable reasoning. Based on the level of uncertainty, i.e., entropy and varentropy, the Entropix system will resample tokens, branch to generate options, perform chain-of-thought, or give the ‘best’ token answer. Early Entropix results look promising.
Entropix presents another approach to sample over inference-time token generation for improved reasoning. This area is ripe for further experimentation and exploration.

SMART: Self-learning Meta-strategy Agent for Reasoning Tasks
Tasks requiring deductive reasoning, especially those involving multiple steps, often demand adaptive strategies such as intermediate generation of rationales or programs, as no single approach is universally optimal. While Language Models (LMs) can enhance their outputs through iterative self-refinement and strategy adjustments, they frequently fail to apply the most effective strategy in their first attempt.
As quoted above, LLMs have a big challenge in reasoning, in that there are many reasoning strategies that could be applied, but it’s hard to get it right on the first attempt. The paper SMART: Self-learning Meta-strategy Agent for Reasoning Tasks introduces the SMART (Self-learning Meta-strategy Agent for Reasoning Tasks) framework, designed to improve LLM accuracy on deductive reasoning tasks by helping the choose the best strategy on the first attempt.
SMART models the strategy selection problem as a Markov Decision Process (MDP). The LLM acts as an agent, selecting a strategy (action) from a set including Chain-of-Thought (CoT), Least-to-Most (L2M), or Program-of-Thought (PoT). The LLM learns a policy to maximize its expected reward using reinforcement learning, updating its strategy selection based on past performance.
Experiments on reasoning datasets like GSM8K, SVAMP, and ASDiv, using LLMs such as Gemma 7B, Mistral 7B, and Qwen2 7B, show significant improvement over baseline models using 8-shot prompting and iterative refinement. SMART achieves up to a 15-point gain on GSM8K and generalizes to out-of-distribution datasets.
SMART demonstrates improved performance as a refinement strategy compared to traditional refinement methods and shows the efficacy of dynamic context-based strategy selection compared to just applying a fixed strategy.

Talker-Reasoner: Agents Thinking Fast and Slow
One of the dichotomies of LLM usage is that often we use LLMs just for a simple, linear task, such as a summarization task or factual question, whereas other queries might require deeper thought. This dichotomy has been recognized as a parallel to the System 1 and System 2 thinking described by Kahneman in “Thinking Fast and Slow.”
The paper Agents Thinking Fast and Slow: A Talker-Reasoner Architecture introduces a novel "Talker-Reasoner" architecture for AI agents to explicitly address these dual requirements of AI agents: Engaging in natural language conversation and performing deliberative planning and reasoning.
The "Talker" agent (System 1) handles rapid, intuitive conversational responses, leveraging available information and memory. The "Reasoner" agent (System 2) performs slower, more logical multi-step reasoning, planning, tool use and actions. Both systems are implemented with an LLM.
The authors evaluated their architecture in a sleep coaching scenario, examining its strengths and limitations. The Talker excels in initial conversational exchanges. However, for tasks requiring complex planning (e.g., generating a multi-step sleep improvement plan), the Talker's reliance on older belief states can lead to "snap judgments." In such cases, the Talker is instructed to wait for the Reasoner, simulating System 2 overriding System 1.
This work, like prior works mentioned above, suggests that context is important for deciding how and when to apply AI reasoning techniques. This is an obvious conclusion, but less obvious is how an AI model or agent should decide on-the-fly during inference which techniques to apply. AI researchers are diligently developing solutions to this challenge, as the race to advance AI reasoning continues.