AI Research Roundup 24.09.19 - Reasoning
Rest-MCTS for LLM self-training, LLM monkeys scale inference compute, REAP for LLM problem solving, enhanced LLM agent decision-making with Q-value models, diagram of thought.
Introduction
The release of o1 last week has put LLM reasoning time of mind. This week, we cover new research results in this area:
ReST-MCTS*: LLM Self-Training via Process Reward Guided Tree Search
Large Language Monkeys: Scaling Inference Compute with Repeated Sampling
Enhancing LLM Problem Solving with REAP: Reflection, Explicit Problem Deconstruction, and Advanced Prompting
Enhancing Decision-Making for LLM Agents via Step-Level Q-Value Models
On the Diagram of Thought
In addition to these papers that we’ll cover, the paper “Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters” from Google DeepMind is getting attention now because it quantifies test-time compute scaling, similar to what OpenAI used in o1. We covered this paper in our AI Research Roundup in mid-August. It’s worth a second look. It highlights the potential of test-time compute scaling for improving LLM performance and evaluates different approaches.
This latest research from AI labs and academic groups is solving LLM reasoning; it gives me confidence multiple LLMs with advanced reasoning powers are coming soon.
ReST-MCTS*: LLM Self-Training via Process Reward Guided Tree Search
The paper “ReST-MCTS*: LLM Self-Training via Process Reward Guided Tree Search” introduces a novel approach to enhance LLM reasoning with reinforced self-training called ReST-MCTS*. The method is based on integrating process reward guidance with a tree search algorithm, MCTS*, to gather superior reasoning traces and per-step value estimations. These are then leveraged to refine both policy and reward models.
As in prior work on LLM reasoning, they use process reward model (PRM) to train reasoning paths. However, a key challenge in LLM self-training with PRM is properly judging and annotating the intermediate steps. They ask, “How can we automatically acquire high-quality reasoning traces and effectively process reward signals for verification and LLM self-training?”
Their solution is to use Monte Carlo tree-search (MCTS) to estimate correctness of a process step:
ReST-MCTS* circumvents the per-step manual annotation typically used to train process rewards by tree-search-based reinforcement learning: Given oracle final correct answers, ReST-MCTS* is able to infer the correct process rewards by estimating the probability this step can help lead to the correct answer.
Thus, ReST-MCTS* eliminates the need for manual per-step annotations and instead infers correct process rewards, by estimating probability that a given step contributes to the correct answer. These inferred rewards are then utilized to refine the PRM and select high-quality traces for policy model self-training.
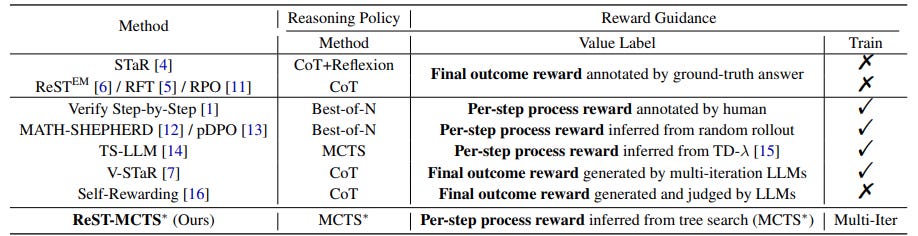
Experimental evaluations demonstrate that ReST-MCTS* outperforms prior LLM reasoning baselines and self-training algorithms, achieving higher accuracy on math and reasoning benchmarks compared to previous methods.
Large Language Monkeys: Scaling Inference Compute with Repeated Sampling
The paper Large Language Monkeys: Scaling Inference Compute with Repeated Sampling explores the topic of inference or test-time compute as a new scaling paradigm for LLMs. More specifically, they investigate the concept of scaling inference compute by leveraging repeated sampling. It’s a simple idea: Generate multiple samples (answers) per problem instead of relying on a single inference pass, thereby increasing the likelihood of finding a correct solution.
What performance results do they observe from scaling inference?
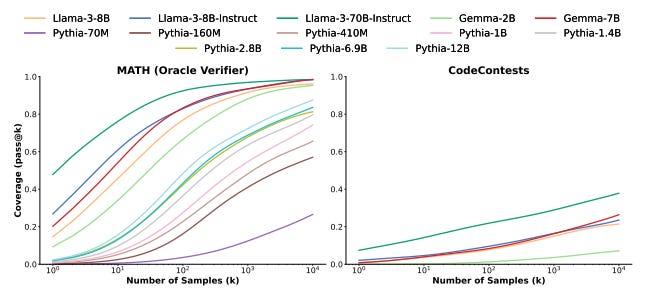
Across multiple tasks and models, we observe that coverage - the fraction of problems solved by any attempt - scales with the number of samples over four orders of magnitude. In domains like coding and formal proofs, where all answers can be automatically verified, these increases in coverage directly translate into improved performance.
Note that this is not a ‘smart’ sampling or reasoning method, but simply brute-force repetition. Yet it exhibited improvement across a broad sample of tasks and LLMs over 4 orders of magnitude,. As the authors note:
Interestingly, the relationship between coverage and the number of samples is often log-linear and can be modelled with an exponentiated power law, suggesting the existence of inference-time scaling laws.
They validated the concept that inference-time compute can scale performance in a number of experimental results, sharing charts that show the log-linear relationship between number of samples and coverage (performance).
They also achieved state-of-the-art results on the SWE-bench Lite dataset by applying repeated sampling to a less capable model, outperforming single-attempt solutions from more powerful models:
When we apply repeated sampling to SWE-bench Lite, the fraction of issues solved with DeepSeek-V2-Coder-Instruct increases from 15.9% with one sample to 56% with 250 samples, outperforming the single-attempt state-of-the-art of 43% which uses more capable frontier models.
The random sampling approach is effective for tasks with automatic verification mechanisms like coding or formal proofs, as you can check any generated answers. However, it is impractical in cases where you cannot verify a correct solution. Further research into effective verification methods would help address that hurdle and harness the benefits of repeated sampling for more tasks.
Enhancing LLM Problem Solving with REAP: Reflection, Explicit Problem Deconstruction, and Advanced Prompting
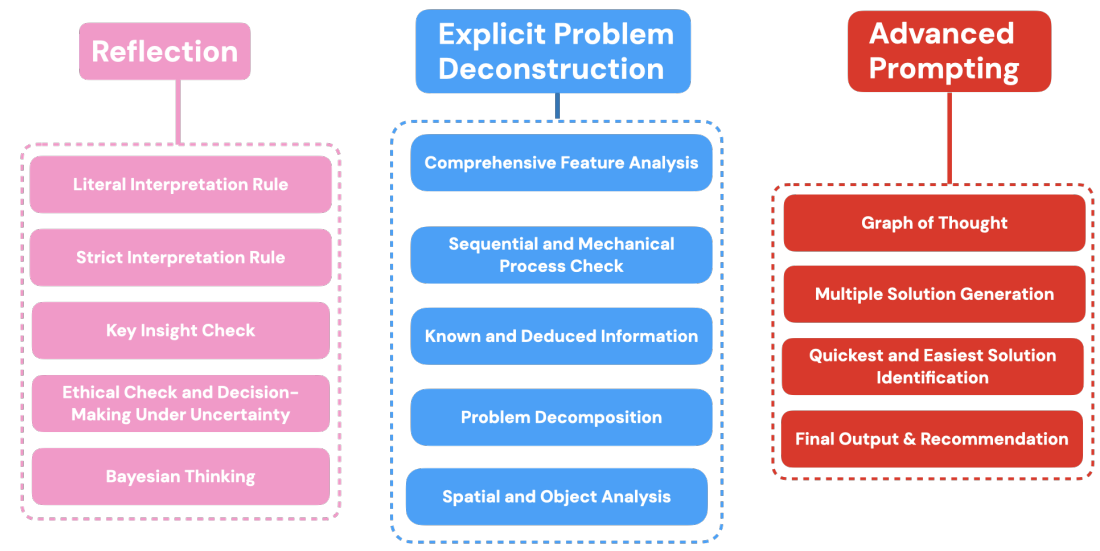
The paper “Enhancing LLM Problem Solving with REAP: Reflection, Explicit Problem Deconstruction, and Advanced Prompting” comes from Honda Research USA and presents the REAP methodology, designed to enhance LLM problem-solving.
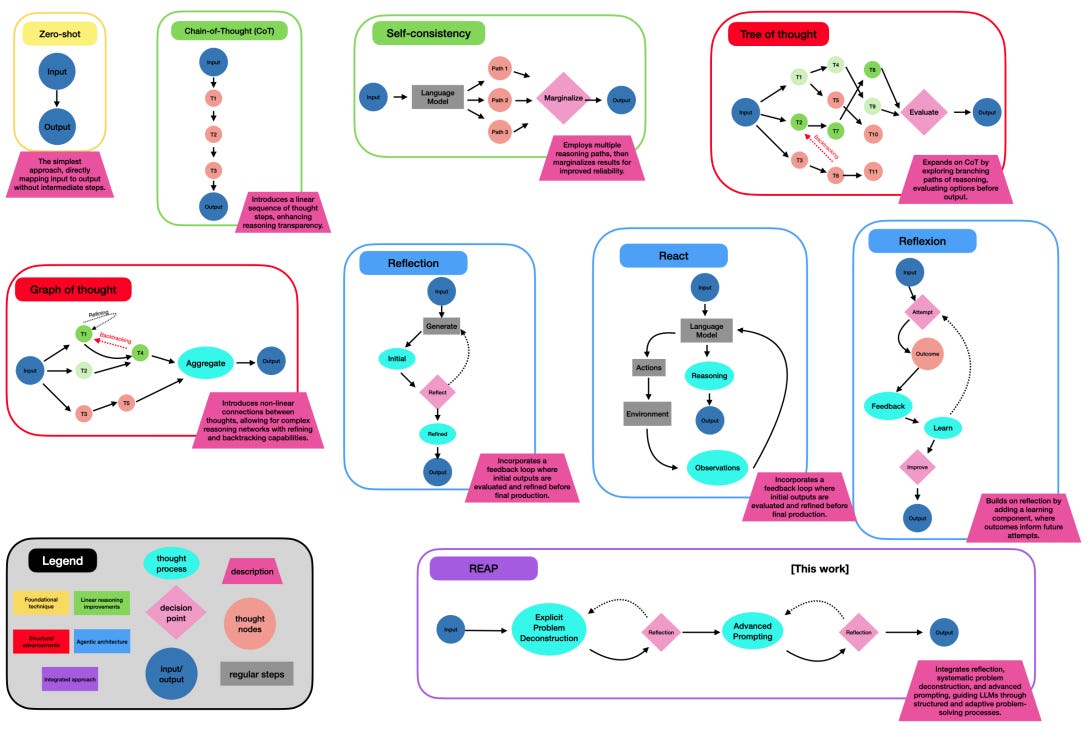
REAP operates within the dynamic context generation framework and guides LLMs through a structured process of reflection, explicit problem deconstruction, and advanced prompting. This approach aims to improve the quality, coherence, and relevance of LLM-generated outputs, particularly for complex, reasoning-intensive tasks.
REAP's core components include:
Reflection: Encourages the LLM to continuously reassess and refine its approach during problem-solving, ensuring adherence to explicit information and ethical considerations.
Explicit Problem Deconstruction: Systematically breaks down complex tasks into smaller, manageable units, facilitating a structured analysis and enhancing the LLM's understanding.
Advanced Prompting: Directs the LLM's reasoning through a combination of strategies, including the Graph of Thought and Multiple Solution Generation, to explore various solution pathways and produce coherent, contextually appropriate outputs.
The authors evaluated REAP using a dataset designed to expose LLM limitations, comparing zero-shot prompting with REAP-enhanced prompts across six state-of-the-art models: OpenAI's o1-preview, o1-mini, GPT-4o, GPT-4o-mini, Google's Gemini 1.5 Pro, and Claude 3.5 Sonnet. They shared detailed prompting results in a 500-page long Appendix.
The results demonstrate notable performance gains, with o1-mini improving by 40.97%, GPT-4o by 66.26%, and GPT-4o-mini by 112.93%.
Even o1-preview showed some (modest) gains. REAP also proved to be cost-effective, enabling cheaper models to deliver competitive results. Additionally, REAP improved the clarity of model outputs, making it easier for humans to understand the reasoning behind the results.
REAP presents a promising approach to significantly enhance the problem-solving capabilities of LLMs, by combining and enhancing prior methods (decomposition, reflection, graph-of-thought) to yield improved performance and cost-efficiency.
Enhancing Decision-Making for LLM Agents via Step-Level Q-Value Models
Agents significantly extend LLM capabilities by perceiving environments, making decisions, and taking actions but still face challenges in complex decision-making. That challenge has led to problems with AI agent reliability, limiting their utility.
The paper Enhancing Decision-Making for LLM Agents via Step-Level Q-Value Models shows how step-level Q-value models can significantly improve decision-making for LLM agents. Q-value functions, widely adopted by Reinforcement Learning (RL) agents, are trained to estimate the value of specific actions. The authors propose a novel method to guide action selection using step-level Q-value models:
Specifically, we first collect decision-making trajectories annotated with step-level Q values via Monte Carlo Tree Search (MCTS) and construct preference data. We then use another LLM to fit these preferences through step-level Direct Policy Optimization (DPO), which serves as the Q-value model. During inference, at each decision-making step, LLM agents select the action with the highest Q value before interacting with the environment.
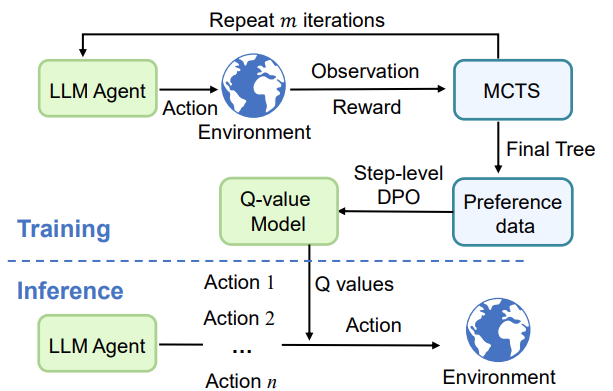
Applying their proposed Q-value model to various open-source and API-based LLM agents on web navigation (WebShop) and question-answering (HotPotQA) tasks led to significant performance improvements. Notably, the performance of a Phi-3-mini-4k-instruct based agent improved by 103% on WebShop and 75% on HotPotQA, even surpassing GPT-4o-mini.
Integrating Q-value models mitigates limitations of sparse environmental rewards in complex tasks. These models bring immense efficiency to training—rather than fine-tuning complex LLMs, they effectively guide action choices in just a single trial, making inference faster and simpler.
The authors highlight their method's efficiency, effectiveness, and plug-and-play nature. This approach could redefine how LLM agents operate across various tasks, making them smarter and more efficient. It also suggests commonality between the methods that improve LLM reasoning and those that improve AI agent reasoning.
On the Diagram of Thought
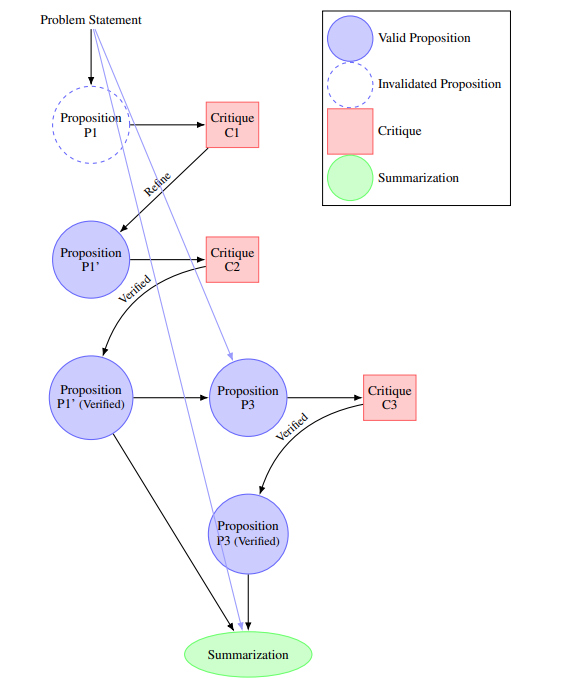
The paper On the Diagram of Thought presents a framework for modeling iterative reasoning within LLMs. Diagram of Thought (DoT) structures the reasoning process as the construction of a Directed Acyclic Graph (DAG), where nodes represent propositions, critiques, refinements, and verifications, and edges denote logical relationships.
DoT employs three internal roles managed by the LLM using auto-regressive next-token prediction: the Proposer, which generates new propositions; the Critic, which evaluates and critiques propositions; and the Summarizer, which synthesizes validated propositions into a coherent final output:
Each node in the diagram corresponds to a proposition that has been proposed, critiqued, refined, or verified, enabling the LLM to iteratively improve its reasoning through natural language feedback.
The paper formalizes DoT using Topos Theory, providing a mathematical foundation offers a robust and general description for representing step-by-step problem-solving.
DoT is a helpful representation framework for the LLM reasoning process, one that allows LLMs to explore complex reasoning pathways while maintaining logical consistency, overcoming limitations of linear or tree-based models. They share code and examples at this https URL.




Thanks again. Great article. Very informative. Good information. Yes indeed.