Getting LLMs To Reason With Process Rewards
The Path to AGI is RL-based and process-reward driven
TL;DR - This article dives into AI research to get LLMs better at reasoning and problem-solving; 8 papers are discussed. Reinforcement learning (RL) based on process-reward model (PRM) is the main approach that has borne fruit to improve LLM reasoning, which is why the speculation around Q* centered around this.
The LLM Reasoning Challenge
There is more to say related to the topic of AI reasoning. In our prior article, “LLM Reasoning and the Rise of Q*,” we outlined some key points:
Today’s LLMs by themselves cannot reason very well. LLMs reasoning is limited by being next-token predictors. The ‘two system’ paradigm from Daniel Kahneman’s "Thinking, Fast and Slow" is helpful on this point. Our minds have two systems of thinking: A fast, intuitive, instant-reaction thought, and a second, slower, more deliberative and logical thought process. Andrei Karpathy has put it, “LLMs only have system one.”
There are many challenges to overcome to get LLMs to reason better. We cannot simply scale LLMs to get to real-world problem-solving and reasoning, we must get them to engage in the ‘system two’ thought process, which will require algorithm breakthroughs.
We can nudge LLMs to reason better through prompting better (“Let’s think step-by-step”), re-prompting, reflection and review. Chain-of-thought spawned further iterations on the idea of breaking down a complex problem: Tree-of-thought, graph-of-thought, skeleton-of-thought, etc. Such methods that explore the search space and reflect on results can nudge LLMs to solve complex problems out of reach from basic prompts.
Fundamentally, reasoning and complex problem-solving is a search-exploration problem; it also involves some level of planning (breaking down a complex problem into parts). As such, it is amenable to RL (reinforcement-learning) that combine search mechanisms.
On this last point, it should be pointed out that the most remarkable AI model achievements in AI reasoning and scientific exploration have been thanks to DeepMind using RL and deep-learning. After using AlphaGo to conquer the game of Go, DeepMind solved the protein-folding problem with AlphaFold, then used AlphaTensor to discover better ways to multiply matrixes beyond what humans were able to achieve.
DeepMind’s latest AI model achievement is using deep learning to discover millions of new crystals, a huge advance in materials science. Can AI make new discoveries or invent something new? It already has, thanks to DeepMind’s AI models.
If we get LLMs to reason, it will be by combining them with the features of these RL-based AI models. But how?
Fine-tuning with the Process Reward Model
One part of this puzzle of LLM reasoning that we want to dig deeper on was touched on explicitly in a write-up on Q* by Nathan Lambert, namely, the Process-supervised Reward Model.
In order to train a model to know what “good” results are, you need to develop a good reward model. But what to reward in a multi-step problem? The Process-supervised Reward Model (PRM) rewards each step of the process of a reasoning solution; it is a finer-grained approach than the Outcome-supervised Reward Model (ORM) that only rewards the final result.
The paper “Solving math word problems with process- and outcome-based feedback” by Uesato et al. (2022) first introduced PRM, highlighting its advantages over ORM in improving LLM reasoning. They applied these reward models to supervised learning with reward model-based reinforcement learning to fine-tune pre-trained language models.
They found that final-answer rates were similar between ORM and PRM, but the best approach was PRM, showing it “significantly improves both trace error rate, from 14.0% to 3.4%, and final-answer error rate, from 16.8% to 12.7%.”
The paper “Let’s Verify Step by Step” from Lightman et al. at OpenAI took the next step. They compared the ORM and PRM, but used more human feedback and took on more challenging tasks. Using pre-RLHF GPT-4 as their base model, their results showed that “process supervision can train much more reliable reward models than outcome supervision,” scoring up to 78.2% of problems from the MATH test set.
The authors showed a large gap in the capabilities of PRM over ORM, wider than shown by Uesato et al. However, they contended that was due to training at larger scale and evaluating more complex tasks.
Math Wizardry with RLEIF
The research in WizardMath: Empowering Mathematical Reasoning for Large Language Models via Reinforced Evol-Instruct extended the use of PRM to improve open source models with fine-tuning for reasoning. Specifically, WizardMath used Llama2 as the base model, then applied their approach, Reinforcement Learning from Evol-Instruct Feedback (RLEIF), in order to fine-tune the model to handle complex math tasks.
Reinforcement Learning from Evol-Instruct Feedback (RLEIF) first uses Evol-Instruct to generate a variety of problems from a base set, then trains both an IRM (instruction reward model) and PRM (process-supervised reward model) to evaluate/reward the problem and the steps towards its solution. These policies are used for fine-tuning the LLM.
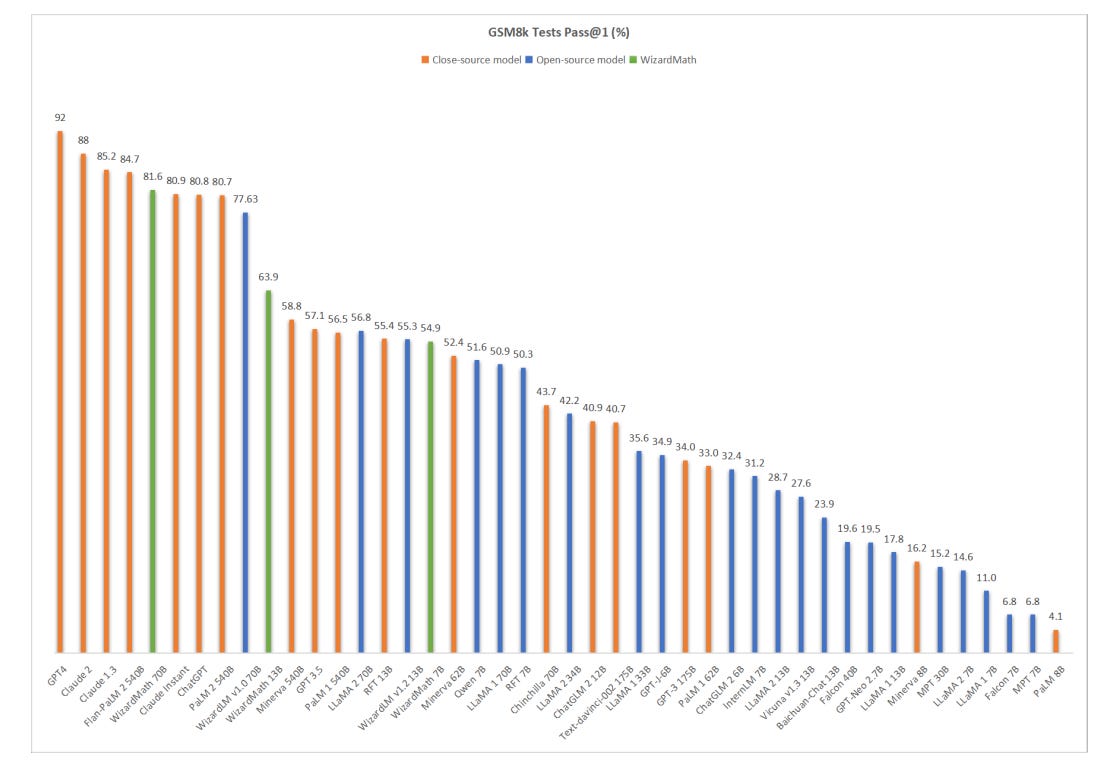
The results are remarkable. WizardMath managed to improve from 56.8 on the base model LLama2 70B to 80.9, besting ChatGPT and closing the gap on the best AI models.
Let’s Reward Step by Step
In October, researchers from Singapore and China presented a further evolution of the PRM idea, with Let's reward step by step: Step-Level reward model as the Navigators for Reasoning.
1. We explored the feasibility of utilizing PRM during the decoding phase. Training and deploying PRM is a challenging task. By demonstrating the viability of PRM-assisted decoding on open-source models, we’ve achieved a significant advancement.
2. We evaluated the strengths and weaknesses of prior methods for enhancing large language model reasoning capabilities. Innovatively, we combined PRM with path search, introducing a heuristic greedy search algorithm that leverages PRM for step-level feedback.
3. Ours is the pioneering effort to apply PRM in the coding domain. We have released a PRM dataset specifically for code and validated that PRM is effective across a broader spectrum of reasoning tasks.
This latter point is of key interest. An alternative approach to solve math problems is to utilize tools, such as code interpreter or data analysis, driven by the LLM. Ask Chat-GPT (GPT-4) a math-related question these days, and it will emit some python code, execute it, and return the answer. If the LLM can reason via code and code via reasoning, it’s a powerful combination.
Moreover, it highlights how a process-based reward system could be used in a number of useful LLM contexts beyond reasoning. For example, if you could ‘score’ an essay by sentence / paragraph, that detailed feedback is more useful for tailoring responses.
Reasoning Scaling on LLMs
The paper “Scaling Relationship on Learning Mathematical Reasoning with Large Language Models” found that pre-training loss correlated with reasoning performance of an LLM, increasing linearly as pretraining loss was reduced. The pretraining of the LLM drives the pretraining loss, and that will dictate the capabilities of reasoning.
They also found a log-linear relation between supervised fine-tuning (SFT) and model improvement, with better / larger models improving less. They used Rejection sampling Fine-Tuning (RFT) which selected correct reasoning paths as an augmented dataset to fine-tune better than SFT:
We find with augmented samples containing more distinct reasoning paths, RFT improves mathematical reasoning performance more for LLMs. We also find RFT brings more improvement for less performant LLMs.
Orca and Orca 2: Learning from Step-by-step
The Microsoft AI model Orca and related paper “Orca: Progressive Learning from Complex Explanation Traces of GPT-4” introduced the idea of using ‘richer signals’ than just the ‘right answer’ in fine-tuning training.
“Orca learns from rich signals from GPT-4 including explanation traces; step-by-step thought processes; and other complex instructions, guided by teacher assistance from ChatGPT.”
Comparing Orca with other 13B fine-tuned models based on a Llama2 13B such as Vicuna, Orca greatly improved on benchmarks like Big-Bench Hard (BBH) and AGIEval. It showed that learning from step-by-step explanations improved LLM reasoning.
Orca 2 extended this work to “employ different solution strategies for different tasks” and was able to further improve the results on reasoning benchmarks, in particular focusing on developing different strategies for problem-solving and training the LLM to learn and apply them for diverse problems.
Conclusion
Applying AI to reasoning has been a core goal in AI research throughout its history. As shown in “A Survey of Deep Learning for Mathematical Reasoning” there has been a lot of effort and progress in using deep learning, but the biggest breakthroughs have come recently with emergent phenomenon of LLMs. The LLMs like GPT-4 show “sparks of AGI” and emergent reasoning capabilities.
While it makes sense to build on LLMs to get AI that can reason, LLM reasoning capabilities are limited, fragile and inconsistent. Robust real human-level reasoning requires augmenting LLMs with other methods. The main advances needed to get to human level reasoning points to RL as the base algorithm and process rewards (PRM) as the appropriate target.
That is why the speculation over Q* pointed to PRM and some form of RL-based reasoning enhancement. This tantalizing quote below from the "Let's Verify Step-by-step" is one more piece of evidence that OpenAI agreed with that assessment.
“We believe that process supervision is currently underexplored, and we are excited for future work to more deeply investigate the extent to which these methods generalize.” - Lightman et al. (2023)
Reasoning is a form of exploration that involves iterative search and feedback. It is not linear. The right search process and correct steps along the way is required to yield correct outcomes. Beyond these methods are the developments of further iterative loops and feedback mechanism outside the LLM query-response loop.
That’s where AI Agents come in, a topic for another day.
Postscript. The Efficiency of Reinforcement Learning
Reinforcement learning (RL) is computationally expensive. The paper “Accelerating Self-Play Learning in Go” from 2019 discusses the large compute used by AlphaZero and other replications. AlphaZero used 41 TPU years to get to superhuman Go performance. This paper cut the computation cost by a remarkable 50x to approximately 1 GPU-year.
The author did it with a “variety of domain-independent improvements that might directly transfer to other AlphaZero-like learning or to reinforcement learning more generally.” These included techniques for pruning the policy targets better, adding auxiliary policy targets, etc. In layman’s terms, determining how to learn better at each step, and save time by pruning the search space better.
This begs the question: What’s the most efficient path to becoming super-human at Go? What’s the minimum number of games needed to play to get there? This too is under-explored. To get to AGI, find ways to further improve the efficiency of RL.






